Срініваса Рамануджан був, можливо, першим з по-справжньо-му «модерних» вчених індійської науки. Він впевнено забезпечив Індії почесне місце у тій бистрині наукових відкриттів, що збурювала Західний світ від початку 17 століття. На той час у математиці Індія вже відзначилася розвитком десяткової системи числення, відкриттям «нуля» та такими солідними іменами як Бхаскара та Брахмагупта. Індійська наукова школа досягла також цікавих результатів та швидких рішень у галузі арифметики. Але абстрактна робота й аналіз, що вимагали систематичності й надавали значення доказам і переходу від конкретних результатів до загальних принципів, були відкриті греками й отримали продовження у західній математиці. Беззаперечно, Індія з давніх чаів вивела на високий рівень май-стерності архітектуру та металургію, але в 19 столітті саме Європа була лідером у багатьох галузях, таких як інженерна справа, суднобудування, хімічні технології, прядіння та ткацтво, … а ще наука!
Система освіти, запроваджена британцями в Індії, базувалася на англійській системі, тож серед іншого викладалися й основи формальної математики. Найздібніші з індійців не тільки досягли успіхів у юриспруденції та торгівлі, в техніці та математиці, але й створили «математичне товариство». Це товариство на-магалося зробити доступними для своїх членів дорогі книги та газети Америки та Англії. Але все-таки метою цієї системи освіти було лише забезпечити британський режим освіченими та кваліфікованими робітниками. Система не намагалася створити філософів і мислителів, що ставилося за мету перед університетами Англії.
Саме за таких, не надто сприятливих умов, Срініваса Рамануджан Аянгар зумів вразити західний світ своїми досягненнями. Він зумів глибоко зануритися у базову та практичну математику, що викладалася в рамках інуючої системи, і осягнути все, чого дошукалися кращі євопейські математики за останні три сотні років. А потім пішов далі і відкрив цілі нові області досліджень та цікавих речей, що вивчаються та аналізуються й по сьогодні.
Рамануджан народився 22 грудня 1887 року в Ероді, на березі Кавері, за 245 кілометрів на південний захід від Ченнаї. Його батько був бухгалтером у компанії, що торгувала сарі та тексти-лем у Кумбаконамі, і, здається, він не мав значного впливу на Рамануджана. Мати Рамануджана була відчутно сильнішою і ви-тонченішою особистістю, тому і в смейних питаннях останнє слово було за нею. Вона була співачкою бхаджанів (релігійних пісень) у місцевому храмі, заробляючи тим кілька додаткових рупій для поповнення сімейного бюджету.
Отже, Рамануджан провів своє дитинство у тихому храмовому містечку Кумбаконам, виховуючись на давніх індуїстських тра-диціях та літературі і в атмосфері храму й давніх релігійних ритуалів, яких тут дотримувалися століттями.
Поки Рамануджану не виповнилося десять років, він відвідував початкову школу «Кангаян». У 1897 році на випускних іспитах він був кращим в окрузі з англійської й тамільської мов, арифметики та географії. А наступного року вступив до вищої школи Town High, де предмети викладалися англійською мовою:
Town High — це навчальний заклад з певними традиціями, шанованими й досвідченими викладачами та високим рівнем випускників. Рамануджан показав високий рівень здібностей вже на ранніх етапах. Не пройшло й року від початку навчання, як він став певною мірою легендою в математиці. Від перших днів шкільні товариші почали звертатись до нього за допомогою та підказками, а вже за рік він міг полемізуати з викладачами. Саме тоді Рамануджан натрапив і на книгу «Тригонометрія» С. Л. Лоні, класичний англійський університетський підручник, який містив дещо ширший та свіжіший матеріал з цього предме-ту. У свої 13 років Рамануджан вже зумів освоїт підручик Лоні і це був подвиг, яким могли б пишатися набагато старші уні.
Невдовзі Рамануджан вивчив багато складних речей, таких як «кубічне рівняння», тему якого остерігалися зачіпати навіть деякі професійні математики. Він легко орієнтувався у таємницях «пі» та «е».
Число Пі, або відношення довжини кола до його діаметра, яке найчастіше представляється як 22/7, примітне тим, що його ніколи, навіть теоретично, неможливо точно визначити. Інше число — «e», пов’язане з тим, як швидко щось, наприклад, банківський депозит, зростає, якщо складний відсоток додається не раз на рік і навіть не раз на місяць, а продовжується з інтервалами, максимально близькими до нуля. Пі та е також дивовижним чином пов’язані між собою за допомогою використання уявних чисел або величин, які включають квадратний корінь з −1!
Складні поняття були близькими супутниками Рамануджана. Старші на дватри роки учні зверталися до нього з проблемами, які вони не могли вирішити тижнями, і він розв’язував їх миттєво!
Тригонометрія, як випливає з назви, вивчає трикутники, і вона розглядає співвідношенням сторін трикутника з кутом між ними. Найточніший спосіб обчислити ці співвідношення — провести зв’язок між кутами, трикутниками та колами і працювати з нескінченно довгими рядами чисел. Під час навчання Рама-нуджан сам розробив такий спосіб обчислення тригонометричних співвідношень і був просто приголомшений, коли згодом ді-знався, що цей метод відкрив Ейлер ще у 18 столітті!
На час закінчення школи Рамануджан, завдяки своєму таланту в математиці, став знаменитістю. Маючи призи та нагороди, у 1904 році він вступив до Державного коледжу, там само у Кумбаконамі, як студент курсу «First Arts» (FA) на умовах стипендії.
Досі, незважаючи на свою славу, здобуту академічними знан-нями Рамануджан поводився як чемний, вихований юнак і завжди слухався матір. До того ж, будучи феноменом у математиці він непогано орієнтувався і в інших предметах. Однак, опинившись у коледжі, Рамаджан настільки занурився в математику, що вона цілковито поглинула саму його сутність і вивела на поверхню вперту, ексцентричну, майже ірраціональну сторону його характеру, через що Рамунаджан не зміг вписатися в систему формальної університетської освіти і кілька років лишався серед гірших студентів.
Така трансформація, імовірно, відбулася під впливом математичної роботи, яку Рамануджан відкрив перед тим, як залишити школу: ця був «Синопсис елементарних результатів чиcтої математики» Карра, збірка важливих математичних висновків, де результати сформульовано просто, без доказів і пояснень. Хоча сама по собі робота не була важливою, книга познайомила молодого та блискучого Рамануджана з чудесами математики, створеними такими великими людьми, як Ньютон, Ейлер і Ла-плас, починаючи з 17 століття. Її автор, Джордж Шобрідж Карр, насправді був математиком із помірними здібностями, який склав свій Синопсис переважно як довідковий том для студентів.
Протягом 18-го та початку 19-го століть студенти-математики в Англії були просто одержимі бажанням усішно пройти надзвичайно жорстке випробування іспитом Кембриджського університету Трайпос (Tripos). Цей іспит вимагав неймовірних умінь вправлятися з найскладнішими темами з математики та складався з набору непростих задач, і розв’язання кожної з них давало студенту додатковий бал. Щоб успішно пройти Трайпос студент мав вирішити кілька таких задач, а хороший рейтинг за результатами іспиту гарантовано забезпечував студенту блискучу кар’єру в обраній професії.
Відповідно, підготовка студентів до цього іспиту стала платним заняттям. Карр мав ступінь магістра математики в Кемб-риджському університеті і був викладачем-ентузіастом, тож після років копіткої роботи зі студентами, що мали опанувати величезні сфери знань, яких вимагали від них умови іспиту, він і склав свій Синопсис — перелік важливих математичних висновків. Очевидно, це був просто величезний каталог теорем і формул, який, можливо, не мав особливої користі, без зв’яку з усім попередньо вивченим матеріалом.
Але для цікавого Рамануджана, який майже інтуїтивно орієнтувався в математиці, Синопсис Карра відкрив чарівний світ нових загадок, до яких інакше йму б довелося іти через роки класичного навчання. Якщо направду, то Синопсис хоч був переліком готових висновків, але подекуди містив і натяк на певні докази. У всякому разі, наведені у ньому результати подавалися у певній «прогресії», де наступні дані були пов’язані з попередніми. Можливо його не можна наазати коротким викладом історії математики, але все-таки це майже правильний послідовний перелік її найважливіших моментів!
Відсутність детальних доказів змусила Рамануджана знаходити їх самостійно, побіжно відкриваючи нові деталі та розширюючи матеріал. В кінцевому результаті, навчаючись за Карром, Рамануджан проминув засвоєння чіткого методу західної математики, який передбачав чітке формулювання припущень, а потім систематичне отримання висновків з доказами. Натомість, як і Синопсис, велика частина оригінальної роботи Рамануджана складається з блискучих, просто написаних результатів, над якими покоління вчених і студентів, що прийшли після нього, роками ламали голови, аби віднайти докази.
Основним результатом цього знайомства з Карром було те, що під час навчання в коледжі Рамануджан працював над мате-матикою і нічим іншим. Тож коли закінчив курс, його успішність у математиці, звісно, була блискучою, але він провалив англійську мову та мав нікчемні результати з інших предметів. Йому зняли стипендію, і здібний юнак, хоча й намагався якийсь час оплачувати навчання, зводячи кінці з кінцями, але врешті таки мусив залишити Державний коледж у Кумбаконамі.
Наступні місяці були напруженими та неспокійними. Рамануджан виснажував свою сім’ю і був геть не готовий, ні за своїми знаннями, ні за станом душі, до будь-якої оплачуваної роботи. Але потяг до математики не втратив! Врешті-решт Рамануджан почав утікати з дому. Вперше він це зробив у віці 17 років, коли поїхав аж до Вішакхапатнаму, на східному узбережжі Андхра-Прадеш. Що він робив у Вішакхапатнамі і як там себе забезпечував, достеменно не відомо, але за кілька місяців сім’я його розшукала та вмовила повернутись додому. Вочевидь, йому важко було витримати тиск родини, яка вимагала, що він упорядкував своє життя, бо утікав з дому ще кілька разів, поки, вже у віці 19 років, не знайшов собі місце в коледжі Пачайяппа у Ченнаї, щоб іще раз пройти курс FA.
Пачайяппа був закладом з хорошими академічними традиціями та міг похвалитися високим рівнем математичного факуль-тету. Як і раніше, Рамануджан процвітав у математиці, але нехтував усім іншим. Біограф Рамануджана Роберт Канігель в книзі «Людина, яка пізнала нескінченність», повідомляє, що, відповідаючи на запитання про травну систему кроля на іспиті з фі-зіології, Рамануджан нібито написав у своїй екзаменаційній роботі: «Сер, ось мій неперетравлений продукт з розділу про травну систему кроля».
Зайве говорити, що в грудні 1906 року Рамануджан провалив випускний іспит. У наступному 1907 році він знову зазнав невдачі. Єдине, що він міг і умів робити — це навчати студентів математики, хоча й це він робив більшою мірою задля власного задоволення, ніж задля того, щоб допомогти студентам скласти іспити. Тепер це джерело доходу зникло, і Рамануджану більше нічого не залишалося, як жити за рахунок щедрості друзів та родичів. Але він продовжував заповнювати свої зошити математичними формулами.
Рамануджан працював невпинно. Ті самі його зошити списані теоремами та нотатками збереглися і тепер добре відомі. Сьогодні — це велике полотно чистої математики на якому Рамануджан творив свої відкриття протягом цих років. Спочатку він планував подати докази результатів у самому Синопсисі Карра, але скоро пішов набагато далі. Кожна теорема відкривала нові неочікувані аспекти та бачення. У зошитах ми спостерігамо химерне відображення гарячкової різноспрямованої творчості, вираженої у позначеннях, які важко зрозуміти тому, хто не є талановитим математиком. Пізніші зошити — це вже редаговані версії, де матеріал забезпечений коментарями і скомпонований для публікацій. І тим не менше, навіть тут бачимо ті інтуїтивні кроки, стрибки і виражені у найстислішій формі цілі польоти математичної думки, що згодом формували не одне покоління учнів, для яких зчитування цього полотна стало справою всього життя!
Протягом 1908-1912 років Рамануджан працював, наскільки дозволяли йому не надто сприятливі обставини. Він переїхдив із Кумбаконаму до Ченнаї, до Вілліпураму, в район Пондічеррі, чи куди завгодно, де його міг підтримати утримав спонсор чи яка добра душа, і він постійно працював над своєю математикою. Робочі зошити були відредаговані та упорядковані, як візитівка, щоб була змога знайти хоч якусь роботу, яка б забезпечила йому дворазове харчування. Йому також вдалося опублікувати свої перші, досить цікаві статті в журналі Індійського математичного товариства.
Ці ранні документи стосувалися, як і більшість його робіт, рядів чисел, що тягнуться до нескінченності. Наприклад таке число:
або ж квадратний корінь, який містить квадратний корінь, який містить квадратний корінь, і так далі. Коли це було опубліковано в журналі як завдання, щоб кинути виклик читачам, жодного рішення не з’являлося місяцями!
Зміст зошитів і робіт Рамануджана складається з загальних теорем і схем для вирішення таємниць такого роду, а також досліджень властивостей лабіринту математичних констант і математичних функцій, з яких деякі були вже відомі, а інші відкриті ним самим.
Ці публікації Рамануджана швидко почали отримувати ви-знання, і він почав гуртувати навколо себе друзів і шанувальників. Нарешті у 1912 році, за допомогою декого з них, Рамануджан отримав роботу клерка в портовому тресті Мадраса. Маючи регулярну зарплату, він нарешті зміг серйозно присвятити себе математиці. Йому було вже 25 років — вік, в якому математики зазвичай вже працюють за основною спеціальністю, і Рама-нуджану довелося поспішати, щоб наздогнати втрачене!
Саме тоді робота Рамануджана привернула увагу освічених англійців, які працювали в Мадрасі, і вони надіслали частину його робіт поважним математикам в Англії, щоб дізнатися їхню думку. Відповідь була нерішучою та обережною, але такою, що переконала Рамануджана: саме в Англії він повинен шукати про-фесійної оцінки, критики та настанов для своєї подальшої роботи.
Тож Рамануджан почав надсилати видатним математикам Англії листи зі зразками своїх робіт. Напочатку здавалося, що вони ні в кого не викликали інтересу, аж доки блискучий молодий математик з Кембриджа Дж. Г. Гарді таки зацікавився отриманою кореспонденцією і був вражений неймовірною оригінальністю матеріалу, надісланого йому незвичайним індійським клерком.
Далі настав історичний момент. Гарді розпочав процедуру запрошення Рамануджана до Кембриджа ще до того, як відповів на його лист.
Спочатку Рамануджан вагався. Адже ортодоксальні індуси вважали, що перетин океану призводить до втрати своєї касти. Але лист Гарді таки вселив у нього нову впевненість і бажання бути визнаним. Гарді та Рамануджан розпочали переписку стосовно проблем математики, і завдяки цьому спілкуванню в 1913 році Рамануджан отримав запрошення працювати в Універси-теті Мадраса зі стипендію в 50 рупій на місяць. У 1914 році Університет запропонував Рамануджану стипендію в розмірі 250 фунтів стерлінгів для роботи в Кембриджі з додатковими 100 фунтами стерлінгів на переїхд. Рамануджан виїхав до Англії.
У Кембриджі Гарді зміг безпосередньо ознайомитися з диво-вижними зошитами Рамануджана, що містили теореми, близько 120 з яких на той час були йому відомі завдяки їхньому листуванню. І скоро він зрозумів суть побаченого. Значною мірою робота Рамануджана повторювала те, що було відкрито раніше, зокрема протягом тих 40 років, які минули після публікації Синопсису Карра. Деякі частини були навіть неправильними. Але більш як третина роботи, на думку Гарді, була блискучою та абсолютно новою! Інші дослідники вважають цю частку майже половиною.
Харді з усією серйозністю взявся за редагування зошитів Ра-мануджана для публікації. Рамануджан зі свого боку почав працювати в електрифікованому академічному середовищі Кембриджа. Тепер Рамануджан знав, що належна університетська освіта, у тій самій Англії, дала б йому знання з різних областей математики, які були відкриті талановитими людьми до нього. Це не тільки врятувало б його від клопоту безславно відкривати їх знову, але й підштовхнуло б до значно більших речей. У 1915 році, через рік після свого прибуття до Англії, Рамануджан опублікував купу статей, багато з яких містили нові оригінальні дослідження.
Ці статті та роботи наступних років охоплювали нові підходи до оцінки випадкових і нескінченних чисел у розкладі числа π, модульних форм, розбіжних рядів, еліптичних інтегралів, теорії чисел, відкриттів у простих числах, розчленуваннях, круглих числах… Ці теми захопили сучасних математиків, а унікальний підхід Рамануджана та його величезна інтуїтивна чутливість до чисел справили глибоке враження і викликали значний інтерес.
Важливість цієї роботи змусила Гарді запропонувати Рамануджана до обрання членом Трініті Коледжу. Та ньюанси університетської політики і, можливо, певні вияви расизму стримували обрання Рамануджана протягом двох років поспіль. Це боля-че вразило його дух. Щодо тіла, то й воно теж було не в найкращому стані. Через холодні англійські зими Рамануджан захворів на туберкульоз.
Незабаром після розчарування щодо Трініті він потрапив у Метлок, до санаторію де лікували туберкульоз. Але санаторій не надто міг йому допомогти, тому що Рамануджан був переконаним вегетаріанцем і тепер йому дуже бракувало звичної для мешканців південної Індії їжі. Він був надто хворий, щоб продуктивно займатися математикою і це його теж гнітило.
Тим часом, не збентежений невдачею з Трініті, Гарді продов-жував добиватися для Рамануджана визнання, на яке той заслуговував. У грудні 1917 року Рамануджан був обраний членом Лондонського математичного товариства. А ще через два тижні, Гарді та одинадцять інших провідних діячів математики Англії висунули Рамануджана на обрання членом Королівського товариства!
«Відзначився як чистий математик, особливо за його дослідження еліптичних функцій і теорії чисел», як було описано в їхній номінації. У січні 1918 року Королівське товариство опублікувало список із 103 кандидатів, і Рамануджан у цей список увійшов.
Зрозуміло, що тут Рамануджан зіткнувся з серйозними труднощами, не кажучи вже про те, що обрання до Королівського товариства у 31 рік виглядало передчасним. Однак Гарді виявив неабияку наполегливість, стверджуючи, що особу Рамануджана не можна ігнорувати. «Між ним та іншими кандидатами в математиці величезна прірва…»
У лютому цього ж року Рамануджан був обраний членом Кем-бриджського філософського товариства. А потім, через десять днів, Рамануджан насилу повірив телеграмі, яку отримав від Гар-ді: його таки обрали членом Королівського товариства! Через кілька місяців і Трініті Коледж також зробив його своїм стипендіатом.
Все це, як і можна було собі уявити, позитивно вплинуло на моральний стан Рамануджана і за словами Е. Х. Невілла, професора математики в Кембриджі, призвело до «короткого періоду блискучих відкриттів». До слова, Невілл вперше зустрів Рамануджана в Ченнаї у 1914 році, а згодом також зіграв важливу роль у тому, щоб Рамануджан був помічений і почав працювати у Кембриджі.
Здоров’я Рамануджана також, здавалося, дещо покращилося. Після закінчення світової війни, коли морські шляхи були знову відкриті, Рамануджан мав повернутися до Індії, що він і зробив у березні 1919 року.
Він прибув до Індії, як повідомляв журнал Індійського математичного товариства, «з не найкращим станом здоров’я». Про-тягом року після повернення Рамануджан трохи переписувався з Гарді на тему «тета-функції», складної області математики, що включає нескінченності та еліптичні співвідношення, — якраз те, що треба для збурення неспокійних умів. Але здоров’я його потроху погіршувалось, аж поки, 26 квітня 1920 року він і помер, лишившись одним з найоригінальніших математиків століття.
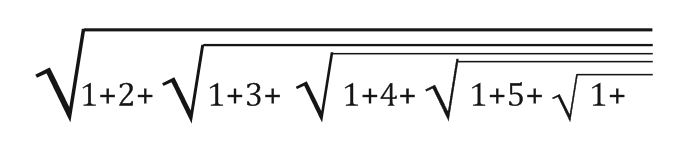




 історія та історичні біографії, геополітика та інформаціний простір, аналітика
історія та історичні біографії, геополітика та інформаціний простір, аналітика



